SSH Encryption

Secure Shell (SSH) is a cryptographic network protocol meant to secure communications over an insecure connection between network devices. One of the ways SSH does this is by using a hybrid approach between asymmetric public/private key- and symmetric cryptography.

SSH is most commonly used as a means for secure remote login and command execution, often in the context of a client-server interaction, but is also often used for authentication and in file transfers protocols (SFTP / SCP).

This article will discuss and explore, among other things, the possible ways of creating SSH-keys, the underlying methods of encryption and some general best practices concerning interactions with servers and ssh key management. It is therefore complementary to the article: "SSH for beginners."

Introduction

A cryptographic system like SSH is used when communications must be withheld from third parties (confidentiality), the identity of the other party needs to be verified (authenticity) and/or when you want to make sure that received messages have not been altered (integrity). To understand how communications are encrypted in SSH we first need to understand some basic terms and concepts. The difference between asymmetric and symmetric cryptography is a good place to start.

Symmetric vs Asymmetric

Symmetric cryptography is something probably most people are and have been familiar since their youth. An example: The alphabet has 26 characters and we assign each position a number (a='1', b='2' etc.), then we proceed to "shift" or "rotate" each character for n steps down this sequence. If we take n=1 for example, so that each letter gets "bumped up" one value and effectively taking the place of the character that was there before. This gives: z='1', a='2', b='3' etc). This algorithm is referred to as ROTn (or Caesar Cipher) where n would be the number of steps to rotate the characters. N would simultaneously be both the key to encrypt and to decrypt the message (hence the name 'symmetric'). An example message would be "Hello World", which we would encrypt with ROT13 to "Uryyb Jbeyq" and could decrypt with the same key back to "Hello World". Many people have experimented with this algorithm to encrypt messages during childhood and almost all people discover quite quickly how easy it is to break such encryption. Of course many more complicated versions exist which are not as easily solved by hand but suffer the same underlying weaknesses as this simplified algorithm does and can get cracked quite easily with modern computing power using methods like frequency analysis. The stress here is on keeping the key a secret, available only to the trusted parties and this is where the distinction with asymmetrical cryptography comes into play.

Asymmetric cryptography, using different keys to encrypt and decrypt, still works very similarly to what we have discussed before. There is an encryption algorithm available (previously the ROTn algorithm but in next parts we will discuss others like RSA and Ed25519) which "jumble" up the message depending on the specific key that is provided (this key will be known as the "public key" from now on) but where it differs is the decryption. Technically speaking the public key used to encrypt still contains all of the information needed to decrypt the message but this information is obfuscated by complexity and a modern computer's inability to retrieve this information in an acceptable amount of time. The other key in the pair (known as the "private key" from now on) is created alongside with the public key and allows for quick decryption of the message. This difference in decryption speed allows for safe sharing of public keys so that anyone wanting to send private data can encrypt it but only the holder of the private key can decrypt easily. The analogy that often comes up is that of the padlock and key: anyone who is provided a padlock (public key) can lock a message in a box, but only the person with the key (private key) is able to open the box and read the message.

Mathematical Concepts

To fully grasp the mathematical complexities of modern-day cryptographic systems one has to delve deep into number theory. This however, falls outside of the scope of this article and we will therefore only superficially touch on these subjects. Two concepts needed to start understanding these are modulo and primes.

When two integers are divided we obtain a quotient (e.g. how often the integer fits in the other) and a remainder. For example 19/5 = 3 with remainder 4, the remainder is referred to as the modulo. In different notation this becomes: 19mod5 = 4.

Prime numbers are positive integers which are only divisible by 1 and themselves (leaving 0 as remainder). The unique-prime-factorization theorem states that any positive integer greater than 1 can be written as a unique product of prime numbers. These are important ideas to keep in mind when moving on to the next part where we will discuss the inner workings of the RSA-algorithm.

RSA vs Elliptic Curve

   !Warning! It is highly advised to trust standardized implementations of the following methods and not write your own. 

RSA

A message can be encrypted into a cipher text (C) if we first represent it as a number (M) according to a character encoding standard like ASCII. Here each character is represented using 7 bits for a total of 128 unique characters, although other encoding standards are available (UTF-8 / -16, extended ASCII etc.) which use more bits per character and thus support a greater variety of characters. "Hello World" would turn into the following sequence of numbers: "072 101 108 108 111 032 087 111 114 108 100". The RSA algorithm proceeds as follows:

   1) Create a numerical representation of original message (similar to our "Hello World"-example)
   2) Choose two (very large "random") primes p and q, which result into: n = p * q
   3) Choose a number d which is a relative prime of: (p-1) * (q-1).
      By relative prime is meant that the greatest divisor of d and (p-1) * (q-1) must equal '1'. 
      d can be chosen relatively easily by picking a prime number larger than either p or q
   4) Compute a number e using numbers d / p / q and Euclid's Algorithm. e and d are so-called multiplicative inverses.

Fig.1 RSA encryption / decryption

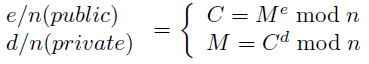
e and n are provided as the public key and are meant to encrypt. d and n are kept as the private key and are meant for decryption. The two formulas presented are used to gain the cipher text from a desired message (encryption) or the message from the received cipher text (decryption). A method to gain the value of M^e / M^d is given by the original authors of the RSA-algorithm by "exponentiation by repeated squaring and multiplication". They refer to volume 2 of Donald Knuth's algorithm bible "The Art of Programming" for more efficient approaches. For an introduction some good materials are also available through the Khan Academy: "Modular Exponentiation".

Example

   1) We have a message "Hello World" which we will translate into numerical values.
      
   2) We choose a prime p = 5  and a prime q = 11. The product of these two result in n = p * q = 5 * 11 = 55.
   3) t = (p-1) * (q-1) = 4 * 10 = 40. This gives us some options to choose a value d, in this case we choose d = 23.

   At this moment we know almost every number needed for both encryption and decryption of our secret message. 
   Only e has still to be computed. This is done using Euclid's Extended Greatest Common Divisor-algorithm.
   e's relation to d is described as such: e * d mod n = 1.

   Figure 3 displays the example worked out, producing the value of e = 7. 
   The following video describes the algorithm in a practical way: "RSA Walkthrough"
   The only difference is in choosing e in the beginning and deducing the value of d, but the method stays the same.

   Now that we have our desired values we can start encrypting our message.
   The first character of our message = 'H'. This is the 8th letter in the alphabet so let's say 'H' = 8.
   To get the cipher text value we have to raise the numerical value of each character to 7 and get the modulo of 55.

   The numerical values of our message are originally (without space character): "08 05 12 12 15 23 15 18 12 04"
   Encryption: 8^7 mod 55 = 2. And when we continue we get the full new message: "02 25 23 23 05 12 05 17 23 49"
   Decryption takes the inverse, raising to the power d: 2^23 mod 55 = 8. Thereby retrieving our original data.

Fig.2 Certificate signed with 2048-bit RSA

Unfortunately RSA on itself is deterministic and therefore clearly unsafe to use as such. Our example uses small numbers, so obfuscation is introduced by choosing the values of p, q, e / d high enough but related problems would remain. To resolve this, one has to add padding to the encryption to ensure a random-factor in the ciphered message. This ensures that the code could only be broken by an attacker if either n is factored or d is obtained from e.

An additional problem with RSA is that it is very slow compared to symmetric encryption algorithms. It is often used as a way to exchange / create a shared symmetric key to bypass the inherent key-exchange problem symmetric-key based encryption systems have instead of encrypting each piece if information fully with RSA. These created keys are therefore used for authentication while the symmetric keys are used for the actual encryption of the connection and the client-server traffic to ensure confidentiality.

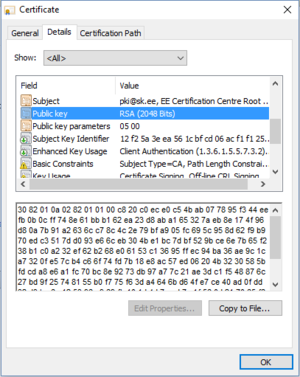
Many more possible problems can arise when using RSA but current implementations are considered very robust. The largest factored RSA-number known stems from 2010 and was 768-bit long. It is estimated that the first 1024-bit keys could be deciphered already and therefore a minimal key length 2048-bits is recommended. Certificates are signed with 2048-bit keys as you can see in figure 2.

Additional information on recommended random number generators / hashing functions are described in "PKCS #1; version 2.2". Interested readers might start looking into schemes like OAEP and NP problems.

Fig.3 Euclid's Algorithm

Elliptic Curve

Fig.4 Elliptic curves following y^2 = x^3 + ax +b. Values 'a' and 'b' are defined.

Fig.5 Geometric addition of two points on an elliptic curve: y^2 = x^3 - 4x + 1. A+B=C'

Fig.6 Geometric addition of two points on an elliptic curve: y^2 = x^3 - 12x. A=B -> A+B=2A=C'

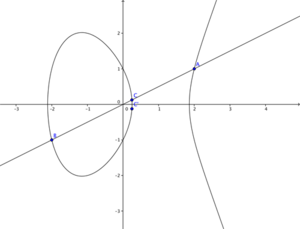
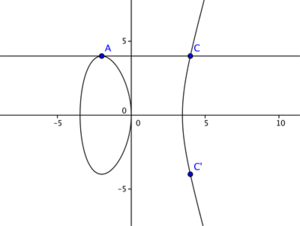
The level of security gained by using an implementation of RSA hinges on the factorization problem of very large numbers, elliptic curve cryptography achieves this security through the "Elliptic Curve Discrete Logarithm"-problem. To illustrate we can consider an elliptic curve of the form: y^3 = x^2 + ax +b. Figure 4 shows an elliptic curve with a range of values for 'a' and 'b' on this curve. Notice the curve where the values a = 0 and b = 0. It produces a "knot" or rather a "singular point" which disqualifies these values for a and b to be considered. Figure 5 starts illustrating how we can obtain public-private key sets by choosing two points on any given curve (A, B), drawing a line between them, determining the intersection with the original curve (C) and mirroring this point on the x-axis, producing the final point (C'). Similarly we can "add" point A and B (both have the same coordinates), take the angle of that point on the curve and produce a third point C which, again-mirrored in the x-axis, produces C'. We can rewrite this as a scalar multiplication: C = 2A. This procedure is seen in Figure 6. The "Elliptic Curve Discrete Logarithm"-problem basically states that scalar multiplication on an elliptic curve is a "one-way-function" by way that if points A and C' are known, it is very hard to determine what the factor (in this case 2) between them is. With hard we again refer to computational time complexity and refer to look into P-NP problems. These examples work with a set of real numbers while in practice this is done with a set of integers.

During the actual process the following domain parameters are public to all (including possible attackers):

 -> The curve itself including the finite field (set of elements described as the modulus of some prime number) and values for 'a' and 'b'.
 -> A generator point G (in figure 6 this was point A).
 -> The size of the list of points this base point creates by scalar multiplication (also known as the order).
 -> Co-factor which is the number of elements on the curve divided by the order (Optimally approaches 1).

When two people (Bob and Alice) want to communicate securely (so that Eve can intercept traffic but not decipher) the following procedure will happen:

 -> Bob will choose a number beta (his private key) which is an integer between 1 and the order-1.
 -> Bob will calculate BETA (earlier point C'), which is a point on the curve. Using the same logic as our earlier example: G * beta = BETA.
 -> Alice will do both these steps for alpha and ALPHA.
 -> Both exchange the calculated coordinates ALPHA and BETA. 
 -> Eve can still hear all of this; she however doesn't know how many "steps" away from the generator point ALPHA and BETA are.
 -> Bob will now multiply the received ALPHA times his secretly chosen number beta and Alice will do the same.
 -> This produces the same new point GAMMA on the curve which only they know, bypassing Eve and leaving her to crack the code.

A great step-by-step video on this process can be found here: "Elliptic Curve Diffie Hellman". This video also goes through some example calculations on how to create cyclic groups, e.g. the points on our chosen curve. In real life these curve parameters are much bigger and often pre-calculated so as to make implementation easier.

OpenSSH allows for two types of elliptic curve public-private key configurations: ECDSA and Ed25519. The former comes in three key-length sizes (256 / 384 or 521 bits) and attempting configuration with altering sizes will fail, while the latter has a fixed-length and depends on implementation. Since the ssh-keygen command still defaults to RSA, one has to indicate specific configuration through the -t switch.

 $ ssh-keygen -t ecdsa -b {256|384|521} 
 $ ssh-keygen -t ed25519

Configuration, Reflection and Conclusion

Configuration ssh-keygen <- RSA is standard 2048-bits. See -b switch.

Certificate authentication using -D and -s switches?

Diffrence private key format in Ed25519 see -o switch

See man page of ssh-keygen for Moduli Generation.

-a switch for KDF "rounds"

Backdoors in random number generators / nsa

See Also

• The original papers on public-private key based cryptography and the RSA algorithm provide an essential starting point for further reading on the topic: "RSA" / "New directions in Cryptography - by W. Diffie and E. Hellman"