SSH Encryption: Difference between revisions
No edit summary |
|||
| Line 118: | Line 118: | ||
==Configuration, Commands and Considerations== | ==Configuration, Commands and Considerations== | ||
We can obtain the public keys provided by a server without connecting to it by using the following command. There are usually more than one provided to retain compatibility. (Enos server provides 3: ECDSA / Ed25519 / RSA) | We can obtain the public keys provided by a server without connecting to it by using the following command. There are usually more than one provided to retain compatibility. (Enos server provides 3: ECDSA / Ed25519 / RSA) | ||
| Line 129: | Line 130: | ||
Of course these commands can also be used in case a service is performing a SSH Key Audit and you need to find out the hash of your own public key. | Of course these commands can also be used in case a service is performing a SSH Key Audit and you need to find out the hash of your own public key. | ||
===Key Strength=== | |||
OpenSSH allows for two types of elliptic curve public-private key configurations: ECDSA and Ed25519. The former comes in three key-length sizes (256 / 384 or 521 bits) and attempting configuration with altering sizes will fail, while the latter has a fixed-length and depends on implementation.<ref>[http://man.openbsd.org/ssh-keygen]Man-page of ssh-keygen command. Retrieved 30.04.2017</ref> Since the ssh-keygen command still defaults to RSA, one has to indicate specific configuration through the <code>-t</code> switch. | OpenSSH allows for two types of elliptic curve public-private key configurations: ECDSA and Ed25519. The former comes in three key-length sizes (256 / 384 or 521 bits) and attempting configuration with altering sizes will fail, while the latter has a fixed-length and depends on implementation.<ref>[http://man.openbsd.org/ssh-keygen]Man-page of ssh-keygen command. Retrieved 30.04.2017</ref> Since the ssh-keygen command still defaults to RSA, one has to indicate specific configuration through the <code>-t</code> switch. | ||
$ ssh-keygen -t ecdsa -b {256|384|521} | $ ssh-keygen -t ecdsa -b {256|384|521} | ||
$ ssh-keygen -t ed25519 | $ ssh-keygen -t ed25519 | ||
Although a direct comparison is hard to make between the strength of elliptic curves vs. rsa based encryption, safety recommendations of several governmental and independent agencies identify a ~250 bit elliptic curve and a ~3000 bit rsa, factoring modulus key to be of equal strength.<ref>[https://www.keylength.com/en/8/]Keylength recommendations. Retrieved 08.05.2017/ref> | |||
Ed25519 keys use a new OpenSSH format to save private keys upon generation which provides additional resistance to brute-force password cracking. RSA and other key-generation algorithms default to the old format but this is configurable with the <code>-o</code> switch. The ssh-keygen command can then be combined with the <code>-a</code> switch which defines the amount of KDF (key derivation function) rounds used. A higher number of these rounds results in slower passphrase verification. This is possible with any SSH2 protocol key but is not supported by OpenSSH before version 6.5. | Ed25519 keys use a new OpenSSH format to save private keys upon generation which provides additional resistance to brute-force password cracking. RSA and other key-generation algorithms default to the old format but this is configurable with the <code>-o</code> switch. The ssh-keygen command can then be combined with the <code>-a</code> switch which defines the amount of KDF (key derivation function) rounds used. A higher number of these rounds results in slower passphrase verification. This is possible with any SSH2 protocol key but is not supported by OpenSSH before version 6.5. | ||
| Line 147: | Line 151: | ||
$ sudo service sshd restart | $ sudo service sshd restart | ||
===Two Factor Authentication=== | |||
In addition we could require any incoming ssh-connections to complete a two-factor authentication process. There are multiple 2FA systems available for Linux, but a popular open-source package is google-authenticator.<ref>[https://github.com/google/google-authenticator-libpam/]Google Authenticator - Github. | In addition we could require any incoming ssh-connections to complete a two-factor authentication process. There are multiple 2FA systems available for Linux, but a popular open-source package is google-authenticator.<ref>[https://github.com/google/google-authenticator-libpam/]Google Authenticator - Github. | ||
Retrieved 05.05.2017</ref> It uses a PAM module, which is a framework for system-wide user authentication<ref>[https://wiki.archlinux.org/index.php/PAM]PAM - Pluggable Authentication Modules. Retrieved 05.05.2017</ref><ref>[http://www.linux-pam.org/]PAM - Distribution site. Retrieved 05.05.2017</ref>, is available for many distributions / phone operating systems and has been tried and tested now for a number of years. It uses a time-based algorithm, plus a secret key generated upon initial set-up to generate a unique code for each login. To install on Debian-based system: | Retrieved 05.05.2017</ref> It uses a PAM module, which is a framework for system-wide user authentication<ref>[https://wiki.archlinux.org/index.php/PAM]PAM - Pluggable Authentication Modules. Retrieved 05.05.2017</ref><ref>[http://www.linux-pam.org/]PAM - Distribution site. Retrieved 05.05.2017</ref>, is available for many distributions / phone operating systems and has been tried and tested now for a number of years. It uses a time-based algorithm, plus a secret key generated upon initial set-up to generate a unique code for each login. To install on Debian-based system: | ||
Revision as of 08:19, 8 May 2017
Secure Shell (SSH) is a cryptographic network protocol meant to secure communications over an insecure connection between network devices. One of the ways SSH does this is by using a hybrid approach between asymmetric public/private key- and symmetric cryptography. [1]
SSH is most commonly used as a means for secure remote login and command execution, often in the context of a client-server interaction, but is also often used for authentication and in file transfers protocols (SFTP / SCP).
This article will discuss and explore, among other things, the possible ways of creating SSH-keys, the underlying methods of encryption, configuration and some general best practices concerning interactions with servers and ssh key management. It is therefore complementary to the article: "SSH for beginners."
Introduction
A cryptographic system like SSH is used when communications must be withheld from third parties (confidentiality), the identity of the other party needs to be verified (authenticity) and/or when you want to make sure that received messages have not been altered (integrity).[2] To understand how communications are encrypted in SSH we first need to understand some basic terms and concepts. The difference between asymmetric and symmetric cryptography is a good place to start.
Symmetric vs Asymmetric
Symmetric cryptography is something probably most people are and have been familiar with since their youth. An example: The alphabet has 26 characters and we assign each position a number (a='1', b='2' etc.), then we proceed to "shift" or "rotate" each character for n steps down this sequence. If we take n=1 for example, so that each letter gets "bumped up" one value and effectively taking the place of the character that was there before. This gives: z='1', a='2', b='3' etc). This algorithm is referred to as ROTn[3] (or Caesar Cipher[4]) where n would be the number of steps to rotate the characters. N would simultaneously be both the key to encrypt and to decrypt the message (hence the name 'symmetric'). An example message would be "Hello World", which we would encrypt with ROT13 to "Uryyb Jbeyq" and could decrypt with the same key back to "Hello World". Many people have experimented with this algorithm to encrypt messages during childhood and almost all people discover quite quickly how easy it is to break such encryption. Of course many more complicated versions exist [5] which are not as easily solved by hand but suffer the same underlying weaknesses as this simplified algorithm does and can get cracked quite easily with modern computing power using methods like frequency analysis.[6] The stress here is on keeping the key a secret, available only to the trusted parties and this is where the distinction with asymmetrical cryptography comes into play.
Asymmetric cryptography, using different keys to encrypt and decrypt, still works very similarly to what we have discussed before. There is an encryption algorithm available (previously the ROTn algorithm but in next parts we will discuss others like RSA and Ed25519) which "jumble" up the message depending on the specific key that is provided (this key will be known as the "public key" from now on) but where it differs is the decryption. Technically speaking the public key used to encrypt still contains all of the information needed to decrypt the message but this information is obfuscated by complexity and a modern computer's inability to retrieve this information in an acceptable amount of time. The other key in the pair (known as the "private key" from now on) is created alongside with the public key and allows for quick decryption of the message. This difference in decryption speed allows for safe sharing of public keys so that anyone wanting to send private data can encrypt it but only the holder of the private key can decrypt easily. The analogy that often comes up is that of the padlock and key: anyone who is provided a padlock (public key) can lock a message in a box, but only the person with the key (private key) is able to open the box and read the message.
Mathematical Concepts
To fully grasp the mathematical complexities of modern-day cryptographic systems one has to delve deep into number theory. This however, falls outside of the scope of this article and we will therefore only superficially touch on these subjects. Two concepts needed to start understanding these are modulo and primes.
When two integers are divided we obtain a quotient (e.g. how often the integer fits in the other) and a remainder. For example 19/5 = 3 with remainder 4, the remainder is referred to as the modulo. In different notation this becomes: 19mod5 = 4.
Prime numbers are positive integers which are only divisible by 1 and themselves (leaving 0 as remainder). The unique-prime-factorization theorem states that any positive integer greater than 1 can be written as a unique product of prime numbers. [7] These are important ideas to keep in mind when moving on to the next part where we will discuss the inner workings of the RSA-algorithm.
RSA vs Elliptic Curve
!Warning! It is highly advised to trust standardized implementations of the following methods and not write your own.
RSA
A message can be encrypted into a cipher text (C) if we first represent it as a number (M) according to a character encoding standard like ASCII. Here each character is represented using 7 bits for a total of 128 unique characters, although other encoding standards are available (UTF-8 / -16, extended ASCII etc.) which use more bits per character and thus support a greater variety of characters.[8] "Hello World" would turn into the following sequence of numbers: "072 101 108 108 111 032 087 111 114 108 100". The RSA algorithm proceeds as follows:[9]
1) Create a numerical representation of original message (similar to our "Hello World"-example)
2) Choose two (very large "random") primes p and q, which result into: n = p * q
3) Choose a number d which is a relative prime of: (p-1) * (q-1).
By relative prime is meant that the greatest divisor of d and (p-1) * (q-1) must equal '1'. [10]
d can be chosen relatively easily by picking a prime number larger than either p or q
4) Compute a number e using numbers d / p / q and Euclid's Algorithm.[11] e and d are so-called multiplicative inverses.
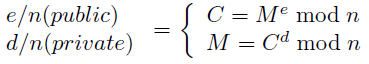
e and n are provided as the public key and are meant to encrypt. d and n are kept as the private key and are meant for decryption. The two formulas presented are used to gain the cipher text from a desired message (encryption) or the message from the received cipher text (decryption). A method to gain the value of M^e / M^d is given by the original authors of the RSA-algorithm by "exponentiation by repeated squaring and multiplication". They refer to volume 2 of Donald Knuth's algorithm bible "The Art of Programming"[12] for more efficient approaches. For an introduction some good materials are also available through the Khan Academy: "Modular Exponentiation".
Example
1) We have a message "Hello World" which we will translate into numerical values.
2) We choose a prime p = 5 and a prime q = 11. The product of these two result in n = p * q = 5 * 11 = 55.
3) t = (p-1) * (q-1) = 4 * 10 = 40. This gives us some options to choose a value d, in this case we choose d = 23.
At this moment we know almost every number needed for both encryption and decryption of our secret message.
Only e has still to be computed. This is done using Euclid's Extended Greatest Common Divisor-algorithm.
e's relation to d is described as such: e * d mod n = 1.
Figure 3 displays the example worked out, producing the value of e = 7.
The following video describes the algorithm in a practical way: "RSA Walkthrough"
The only difference is in choosing e in the beginning and deducing the value of d, but the method stays the same.
Now that we have our desired values we can start encrypting our message.
The first character of our message = 'H'. This is the 8th letter in the alphabet so let's say 'H' = 8.
To get the cipher text value we have to raise the numerical value of each character to 7 and get the modulo of 55.
The numerical values of our message are originally (without space character): "08 05 12 12 15 23 15 18 12 04"
Encryption: 8^7 mod 55 = 2. And when we continue we get the full new message: "02 25 23 23 05 12 05 17 23 49"
Decryption takes the inverse, raising to the power d: 2^23 mod 55 = 8. Thereby retrieving our original data.
Unfortunately RSA on itself is deterministic and therefore clearly unsafe to use as such. Our example uses small numbers, so obfuscation is introduced by choosing the values of p, q, e / d high enough but related problems would remain. To resolve this, one has to add padding to the encryption to ensure a random-factor in the ciphered message. This ensures that the code could only be broken by an attacker if either n is factored or d is obtained from e.[13]
An additional problem with RSA is that it is very slow compared to symmetric encryption algorithms. It is often used as a way to exchange / create a shared symmetric key to bypass the inherent key-exchange problem symmetric-key based encryption systems have instead of encrypting each piece of information fully with RSA. These created keys are therefore used for authentication while the symmetric keys are used for the actual encryption of the connection and the client-server traffic to ensure confidentiality.[14]
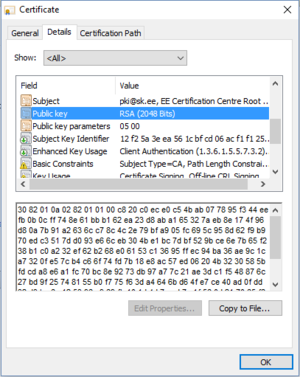
Many more possible problems can arise when using RSA but current implementations are considered very robust. The largest factored RSA-number known stems from 2010 and was 768-bit long.[15] It is estimated that the first 1024-bit keys could be deciphered already and therefore a minimal key length 2048-bits is recommended but higher might be preferable. Certificates are signed with 2048-bit keys as you can see in figure 2.
Additional information on recommended random number generators / hashing functions are described in "PKCS #1; version 2.2". Interested readers might start looking into schemes like OAEP[16] and NP problems[17].

Elliptic Curve

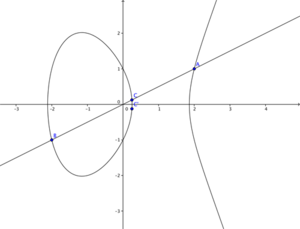
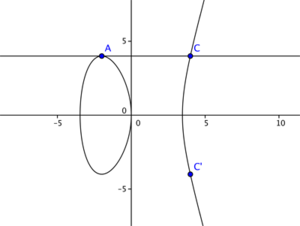
The level of security gained by using an implementation of RSA hinges on the factorization problem of very large numbers, elliptic curve cryptography achieves this security through the "Elliptic Curve Discrete Logarithm"-problem. To illustrate we can consider an elliptic curve of the form: y^3 = x^2 + ax +b. Figure 4 shows an elliptic curve with a range of values for 'a' and 'b' on this curve. Notice the curve where the values a = 0 and b = 0. It produces a "knot" or rather a "singular point" which disqualifies these values for a and b to be considered. Figure 5 starts illustrating how we can obtain public-private key sets by choosing two points on any given curve (A, B), drawing a line between them, determining the intersection with the original curve (C) and mirroring this point on the x-axis, producing the final point (C'). Similarly we can "add" point A and B (both have the same coordinates), take the angle of that point on the curve and produce a third point C which, again-mirrored in the x-axis, produces C'. We can rewrite this as a scalar multiplication: C = 2A. This procedure is seen in Figure 6. The "Elliptic Curve Discrete Logarithm"-problem basically states that scalar multiplication on an elliptic curve is a "one-way-function"[18] by way that if points A and C' are known, it is very hard to determine what the factor (in this case 2) between them is. With hard we again refer to computational time complexity and refer to look into P-NP problems. These examples work with a set of real numbers while in practice this is done with a set of integers.[19]
Diffie Hellman
It is good to note that both algorithms discussed are used for authentication in the ssh process to make sure that both parties can verify who the other is. Upon initial contact the two parties however will first go through a key exchange process to determine a mode of encryption to ensure that all further contact is done in secrecy (confidentiality). This process is called the Diffie-Hellman exchange and is currently done by default with ECDH (Elliptic Curve Diffie-Hellman) in OpenSSH (Although other key exchange protocols are supported) [20]. One more note before moving on: it is important to keep in mind that the public-private keys in Diffie-Hellman and for authentication are not the same.
During the actual process the following domain parameters are public to all (including possible attackers):
-> The curve itself including the finite field (set of elements described as the modulus of some prime number)
and values for 'a' and 'b'.
-> A generator point G (in figure 6 this was point A).
-> The size of the list of points this base point creates by scalar multiplication (also known as the order).
-> Co-factor which is the number of elements on the curve divided by the order (Optimally approaches 1).
When two people (Bob and Alice) want to communicate securely (so that Eve can intercept traffic but not decipher) the following procedure will happen:
-> Bob will choose a number beta (his private key) which is an integer between 1 and the order-1.
-> Bob will calculate BETA (earlier point C'), which is a point on the curve.
Using the same logic as our earlier example: G * beta = BETA.
-> Alice will do both these steps for alpha and ALPHA.
-> Both exchange the calculated coordinates ALPHA and BETA.
-> Eve can still hear all of this; she however doesn't know how many "steps" away from the
generator point ALPHA and BETA are.
-> Bob will now multiply the received ALPHA times his secretly chosen number beta
and Alice will do the same.
-> This produces the same new point GAMMA on the curve which only they know, bypassing
Eve and leaving her to crack the code.
This process not only ensures that any single session is authenticated and secure, but since it initiates this process during each session it also makes sure that if a session-key is broken (by stealing the private key of the session) only that session is compromised but not any others. This is also why one doesn't use the authentication keys to encrypt the session since all sessions would share the same weakness: confidentiality of the private key. [21] Since encrypting each message with this established key is a costly operation, a shared symmetric-key algorithm is negotiated with an accompanying secret key to actually encrypt the rest of the session. To see the list of allowed ciphers in order of preference see: man sshd_config.[22]
A great step-by-step video on this process can be found here: "Elliptic Curve Diffie Hellman". This video also goes through some example calculations on how to create cyclic groups, e.g. the points on our chosen curve. In real life these curve parameters are much bigger and often pre-calculated so as to make implementation easier to use since calculating and then verifying the strength of the curve is a task too heavy for most systems. A good article running through some sample maths hosted on a blog which provides great context: "Elliptic Curves".
Reflection and Conclusion
We have talked so far as to how ssh-keys are created and a little on where they are used, but it is good to describe and repeat how they are used. Let's say we want to connect to a server and we have created our key-pair, how do we authenticate or know for sure that we are talking to the actual server and not a "man-in-the-middle"? How do we ensure integrity and confidentiality in our communications? And which algorithm is safer?
When you create your key-pair you are presented with a Random-art and hashed version of your public key, similarly you will be presented with a hashed version of a server's public key upon initial contact (Old versions use MD5 - later ones default to SHA-256). These hashed versions represent human-readable "non-reproducible" formats of these keys so that one can compare them easily with a publicly published version of that key. Hashes of the server keys can be hosted on a web-server so that anyone who wants to connect to that machine will be able to gain the key information from two separate places and determine that they are one and the same. There is an additional point of authentication that happens upon connection to a server. It presents the client with a message encrypted with its private-key which can be deciphered using the public key that gets presented in parallel. By comparing the hashes of the public key we know it belongs to our specific server while using the public-key to decipher the message verifies that the server is in possession of the accompanying private-key. This all reduces risk, but unfortunately still presumes that you trust the site or source of the published public-key of the server (HTTP vs HTTPS comes into play here) and while you could ask system administrators if no published keys exist, it comes down to your personal judgement whether to trust that source or not. After the known_hosts and authorized_keys files have been checked for the presented keys, the Diffie-Hellman procedure will commence to further encrypt the ssh session and ensure confidentiality.
Data integrity is ensured by a "hash-and-encrypt" method. Each message sent will be run through a hashing algorithm and subsequently encrypted using the party's private key. The receiving party is in possession of the public key and thus able to decipher the hash, run the message through the hashing algorithm and check if the two correspond with each other. This not only ensures data integrity but ensures authenticity of the message. This is called the HMAC (Hash-based message authentication code). The MAC is calculated from the symmetrical shared secret, the packet sequence number of the message, and the actual message content. The hash algorithm is similarly to the session-cipher negotiated right after the Diffie-Hellman key-exchange.[23]
The safety of the algorithms described falls outside of the scope of this article but a few important findings are worth noting. First considering the Diffie-Hellman exchange. Traditional DH uses the same type of process as described but using a RSA-like prime-number based approach. Since computation time can be long for that process it was considered safe to pre-compute certain values as long as bit-values were high enough. It turns out that a very significant portion of the internet was using the same pre-calculated values with 512 and 1024-bit numbers, leaving all systems that did compromised. This vulnerability is known as Logjam[24] and was estimated to break 2/3's of VPN's and 1/4 of all SSH servers globally after breaking just one prime. Recommendations included switching to 2048-bit DH or to ECDH by upgrading to the latest version of OpenSSH.[25]
Elliptic curve is currently considered preferable over RSA but does have some general side notes. As mentioned before, implementations use predefined curves which raises concerns over possibly introduced backdoors. This has happened at least once before in an elliptic curve based random number generator.[26] The "safe-curves" project has been established to ensure access to curves which have been developed in a publicly verifiable way so as to minimize the chance of an introduced backdoor.[27] Future introduction of quantum computers might make RSA more preferable than elliptic curves due to Schor's algorithm.[28]
For more on SSH keys, including possible risks one can visit: "Secure Shell Home".
Configuration, Commands and Considerations
We can obtain the public keys provided by a server without connecting to it by using the following command. There are usually more than one provided to retain compatibility. (Enos server provides 3: ECDSA / Ed25519 / RSA)
$ ssh-keyscan <ip><url>
The hash for these can be obtained using the following commands. Only providing the -l -f switches will provide the default hash depending on the OpenSSH version used, but can be modified with the -E switch.
$ ssh-keygen -l -f <file with server's public-key> $ ssh-keygen -l -f <file with server's public-key> -E md5
Of course these commands can also be used in case a service is performing a SSH Key Audit and you need to find out the hash of your own public key.
Key Strength
OpenSSH allows for two types of elliptic curve public-private key configurations: ECDSA and Ed25519. The former comes in three key-length sizes (256 / 384 or 521 bits) and attempting configuration with altering sizes will fail, while the latter has a fixed-length and depends on implementation.[29] Since the ssh-keygen command still defaults to RSA, one has to indicate specific configuration through the -t switch.
$ ssh-keygen -t ecdsa -b {256|384|521}
$ ssh-keygen -t ed25519
Although a direct comparison is hard to make between the strength of elliptic curves vs. rsa based encryption, safety recommendations of several governmental and independent agencies identify a ~250 bit elliptic curve and a ~3000 bit rsa, factoring modulus key to be of equal strength.Cite error: Closing </ref> missing for <ref> tag[30]
$ sudo nano /etc/ssh/sshd_config
In the configuration of the ssh daemon find the lines "PermitRootLogin" and "PasswordAuthentication" and modify it so that users can only connect with their SSH-key.[31]
PermitRootLogin without-password
or:
PasswordAuthentication no
And restart the service.
$ sudo service ssh restart $ sudo service sshd restart
Two Factor Authentication
In addition we could require any incoming ssh-connections to complete a two-factor authentication process. There are multiple 2FA systems available for Linux, but a popular open-source package is google-authenticator.[32] It uses a PAM module, which is a framework for system-wide user authentication[33][34], is available for many distributions / phone operating systems and has been tried and tested now for a number of years. It uses a time-based algorithm, plus a secret key generated upon initial set-up to generate a unique code for each login. To install on Debian-based system:
$ sudo apt-get install libpam-google-authenticator
Users also need to set-up the Google Authenticator App[35] and create a secret key when they are logged-in on the server. This is done through the following steps:[36]
$ google-authenticator
Do you want authentication tokens to be time-based (y/n) y
<Here you will see generated QR code>
Your new secret key is: ZVZG5UZU4D7MY4DH
Your verification code is 269371
Your emergency scratch codes are:
70058954
97277505
99684896
56514332
82717798
Do you want me to update your "/home/username/.google_authenticator" file (y/n) y
Do you want to disallow multiple uses of the same authentication
token? This restricts you to one login about every 30s, but it increases
your chances to notice or even prevent man-in-the-middle attacks (y/n) y
By default, tokens are good for 30 seconds and in order to compensate for
possible time-skew between the client and the server, we allow an extra
token before and after the current time. If you experience problems with poor
time synchronization, you can increase the window from its default
size of 1:30min to about 4min. Do you want to do so (y/n) n
If the computer that you are logging into is not hardened against brute-force
login attempts, you can enable rate-limiting for the authentication module.
By default, this limits attackers to no more than 3 login attempts every 30s.
Do you want to enable rate-limiting (y/n) y
As you can see one can increase the time any token is valid from 30 seconds to 4 minutes, this might be necessary if delays between client and server are expected. One can also set rate-limiting and allow/disallow the same code to be reused. Obviously these settings as presented would prove most secure. You will now see a series of codes, the first one of which is the secret key one can enter into the app. You can also install libqrencode and it will then display a scannable QR-code.
$ sudo apt-get install libqrencode-dev
The emergency scratch codes are important to note down and keep safe. These will allow you to get back into the system if you were to lose your phone which allows you to run the same $ google-authenticator command again and generate a new secret key. They are stored in the ~/.google_authenticator file for later reference when you are logged in.
This still leaves us with configuring the PAM configuration file on the server. Depending on how you want to use the two-factor authentication one has to either configure the /etc/pam.d/sshd or the /etc/pam.d/system-auth configuration file. We are talking about remote login so the /etc/pam.d/sshd file applies to us, but can be configured globally in the other. Add the following line to the top of that file:
auth required pam_google_authenticator.so
It is important to do so since order matters in this file. Only users who have generated a secret key file will be allowed to log in using ssh. Keep this in mind before implementing the system and inadvertently locking people out.
Configuring SSH is also necessary. Go to your /etc/ssh/sshd_config file and add the following:
ChallengeResponseAuthentication yes
If you disabled password-based authentication and only allow for key-based authentication one has to also add the following:
AuthenticationMethods publickey,keyboard-interactive
Restart the service and you should be ready to go.[37][38]
See Also
- The original papers on public-private key based cryptography and the RSA algorithm provide an essential starting point for further reading on the topic: "RSA" / "New directions in Cryptography - by W. Diffie and E. Hellman"
References
- ↑ [1]"RFC4251". Retrieved 04.04.2017
- ↑ [2]"Kleptography, cryptography with backdoors." Retrieved 04.04.2017
- ↑ [3] "It's important to keep this document secret, so we encrypted it with ROT13, and, for extra security, we applied it twice!" Retrieved 22.02.2017
- ↑ [4]"Mod26". Retrieved 04.04.2017
- ↑ [5] Polyalphabetic Ciphers and how to crack them. Retrieved 22.02.2017
- ↑ [6] Famous cracking of the Nazi Enigma Code using repeated stereotypical messages. Retrieved 22.02.2017
- ↑ [7]Basic proof of prime factorization. Retrieved 06.04.2017
- ↑ [8]ASCII. Retrieved 06.04.2017
- ↑ [9]Original paper describing RSA-algorithm. Retrieved 06.04.2017
- ↑ [10]Euler's Totient. Retrieved 06.04.2017
- ↑ [11]Euclid's Algorithm. Retrieved 06.04.2017
- ↑ [12]The Art of Programming, vol.2 - Knuth. Retrieved 06.04.2017
- ↑ [13]The RSA-problem. Retrieved 07.04.2017
- ↑ [14] Understanding SSH encryption and connection. Retrieved 30.04.2017
- ↑ [15]768-bit RSA-key cracked. Retrieved 30.04.2017
- ↑ [16]OAEP. Retrieved 07.04.2017
- ↑ [17]P vs NP Time Problems by Computerphile. Retrieved 07.04.2017
- ↑ [18]One way functions and the discrete logarithm problem. Retrieved 30.04.2017
- ↑ [19]Introduction of Elliptic Curve Cryptography. Retrieved 30.04.2017
- ↑ [20]Diffie-Hellman. Retrieved 04.05.2017
- ↑ [21]SSH & DH. Retrieved 04.05.2017
- ↑ [22]sshd_config. Retrieved 05.05.2017
- ↑ [23]Hashing in SSH sessions. Retrieved 05.05.2017
- ↑ [24]Logjam. Retrieved 04.05.2017
- ↑ [25]Weak Diffie-Hellman. Retrieved 04.05.2017
- ↑ [26]Dual_EC_DRBG. Retrieved 04.05.2017
- ↑ [27]Safe Curve Project. Retrieved 04.05.2017
- ↑ [28]Schor's Algorithm. Retrieved 04.05.2017
- ↑ [29]Man-page of ssh-keygen command. Retrieved 30.04.2017
- ↑ [30]Hardening SSH. Retrieved 05.05.0217
- ↑ [31]Disable password server-side. Retrieved 05.05.2017
- ↑ [32]Google Authenticator - Github. Retrieved 05.05.2017
- ↑ [33]PAM - Pluggable Authentication Modules. Retrieved 05.05.2017
- ↑ [34]PAM - Distribution site. Retrieved 05.05.2017
- ↑ [35]Set-up 2FA through Google authenticator using App. Retrieved 05.05.2017
- ↑ [36]Google Authenticator - ArchLinux Walkthrough. Retrieved 05.05.2017
- ↑ [37]Digital Ocean - 2FA. Retrieved 05.05.2017
- ↑ [38]Multi-Factor Authentication, Digital Ocean. Retrieved 05.05.2017